Module 2, Practical 10

In this practical we will experiment with programming paradigms.
In particular, we will briefly introduce the dynamic programming technique.

Dynamic programming

Dynamic programming is a strategy to optimize recursive algorithms.
Every time we find an algorithm solving a bigger problem by repetitive recursive calls on smaller subproblems, we can optimize it by using dynamic programming.
The key idea is simply to store in a table the solution of the subproblems and obtain the result of these subproblems by performing a table lookup.

Two approaches exist:

  1. Top-down: solve the problem by breaking it down in smaller subproblems. If the subproblem has already been solved, then the answer has already been saved somewhere. If it has not already been solved, compute a solution and store it. This method is called memoization;

  2. Bottom-up: solve the problem by starting from the most trivial subproblems, going up until the complete problem has been solved. Smaller subproblems are guaranteed to be solved before bigger ones. This method is called dynamic programming.

Consider the classic example of the computation of Fibonacci numbers:

\[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...\]

which can be computed by the following recursive formula:

\[\begin{split}F(n)=\left\{ \begin{array}{ll} n & if\ n == 0\ or\ n\ == 1\\ F(n-1)+ F(n-2) & if\ n > 1 \end{array} \right.\end{split}\]

This problem can be solved with the following recursive code:

[1]:

import time

def fib(n):
    if n <= 1:
        return n
    else:
        return fib(n - 1) + fib(n - 2)


for i in range(20):
    print("Fib({})= {}".format(i, fib(i)))


for i in range(35,40):
    start_t = time.time()
    print("\nFib({})= {}".format(i, fib(i)))
    end_t = time.time()
    print("It took {:.2f}s".format(end_t-start_t))

Fib(0)= 0
Fib(1)= 1
Fib(2)= 1
Fib(3)= 2
Fib(4)= 3
Fib(5)= 5
Fib(6)= 8
Fib(7)= 13
Fib(8)= 21
Fib(9)= 34
Fib(10)= 55
Fib(11)= 89
Fib(12)= 144
Fib(13)= 233
Fib(14)= 377
Fib(15)= 610
Fib(16)= 987
Fib(17)= 1597
Fib(18)= 2584
Fib(19)= 4181

Fib(35)= 9227465
It took 2.57s

Fib(36)= 14930352
It took 4.09s

Fib(37)= 24157817
It took 6.27s

Fib(38)= 39088169
It took 10.34s

Fib(39)= 63245986
It took 17.71s

Although simple to code, the recursive solution performs some steps multiple times, as shown by the following recursion tree (for example f(3) is computed 5 times):

image1

We can use dynamic programming to avoid computing over and over again the same values:

[2]:

import time

def fib_dp(n):
    fib = [0]* (n+1)
    if n > 1:
        fib[1] = 1

    for i in range(2, n + 1):
        fib[i] = fib[i - 2] + fib[i - 1]

    return fib[n]

for i in range(20):
    print("Fib({})= {}".format(i, fib_dp(i)))


for i in range(35,38):
    start_t = time.time()
    print("\nFib({})= {}".format(i, fib_dp(i)))
    end_t = time.time()
    print("It took {:.2f}s".format(end_t - start_t))

#we can even do:
for i in range(1000,1003):
    start_t = time.time()
    print("\nFib({})= {}".format(i, fib_dp(i)))
    end_t = time.time()
    print("It took {:.2f}s".format(end_t - start_t))

Fib(0)= 0
Fib(1)= 0
Fib(2)= 1
Fib(3)= 2
Fib(4)= 3
Fib(5)= 5
Fib(6)= 8
Fib(7)= 13
Fib(8)= 21
Fib(9)= 34
Fib(10)= 55
Fib(11)= 89
Fib(12)= 144
Fib(13)= 233
Fib(14)= 377
Fib(15)= 610
Fib(16)= 987
Fib(17)= 1597
Fib(18)= 2584
Fib(19)= 4181

Fib(35)= 9227465
It took 0.00s

Fib(36)= 14930352
It took 0.00s

Fib(37)= 24157817
It took 0.00s

Fib(1000)= 43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875
It took 0.00s

Fib(1001)= 70330367711422815821835254877183549770181269836358732742604905087154537118196933579742249494562611733487750449241765991088186363265450223647106012053374121273867339111198139373125598767690091902245245323403501
It took 0.00s

Fib(1002)= 113796925398360272257523782552224175572745930353730513145086634176691092536145985470146129334641866902783673042322088625863396052888690096969577173696370562180400527049497109023054114771394568040040412172632376
It took 0.00s

In the latter case we accumulated partial results in a list and re-used them when needed. Consider the following code:

[3]:

import time

def fib_dp(n):
    fib = [0]* (n+1)
    if n > 1:
        fib[1] = 1

    for i in range(2,n + 1):
        fib[i] = fib[i - 2] + fib[i - 1]

    return fib[n]


start_t = time.time()
for i in range(1,15000):
    r = fib_dp(i)
end_t = time.time()
print("It took {:.2f}s".format(end_t-start_t))

It took 33.79s

In this case we repeated the computations several times anyway and had to recompute the solution all the time, which is a little bit of a waste of time. If we are not concerned about using more space we could modify the code in such a way to update a list and return the whole list, ready for a next iteration:

[4]:

import time

def fib_dpV2(n,fibList):
    if n < len(fibList):
        return fibList[n]
    else:
        if n == 0:
            fibList.append(0)
            return 0
        if n == 1:
            fibList.extend([0,1])
            return 1
        L = n - len(fibList)
        for i in range(L):
            # compute all the fibonacci values required to reach fib(n) and store them in the list...
            fibList.append(fibList[-2] + fibList[-1])
        return fibList[-1]


start_t = time.time()
myFibL = []
for i in range(1,15001):
    r = fib_dpV2(i, myFibL)
end_t = time.time()
print("Fibonacci(15000) : {}".format(myFibL[-1]))
print("It took {:.2f}s".format(end_t-start_t))
print("Fibonacci 0..20: {}".format(myFibL[0:20]))

Fibonacci(15000) : 180356212817232358527136269558393274270479577287959770214783776455882580176808282935116449287253001675278567205597341664270703993136851989859494809191272208168671602010135312495296553662790352582033423080689757992520655785610316941531173588408998619812807392167094455165363355259485592278979388870298110870050912172411703995878726547708126588747557108886477742159519675726841476567233617069303168933729769224839193682942110633367322841686836744207977400786184404283243942571683714924012584054120950619420879245008334171878098209414559267738476048405512373264705915648256421029922854826089454770481653365776765021018110912210918296748113016817314353185049893148191072970004722127877580853512230597663125482412037507790122452840808247238862266940374952733301348535189028427982115508256085629078838285854519748549211253115363900979738960948772589014559911367102564396479380119671836661458473444680552841046388920629103926658110037230386547506816712866616340383491227279709660200771238944743897531289959511150305531873160607872566720751381188951153762201432960669039121243742888978686571778654570582578356003787537920689451735958244288072349086881269456351988300299442324421142440230312335818179554507414851349917896307630882698214864014344956780348499120670367075038565963319741348415248138037342603113034434198363994519415494026021710622105031596662576344941382709460665227123428132640271682951472209368453748754510035741638613590279538796566181871895713339174456728394471357415996934436202565485732749272347348991793493320243181956465786389970599533658454386144770652584880176519203467064567384636418219255416950945755037995377546451320680325530900980211314010182766809827492194845387482751225482662997765661866262382112219008183345652570682633899549560294736097218086788785294700336993482784319083980440026327099112563241621005721911339313568395785607613027063516725870186041444932874242502339316433484868302535616417673857358757000197098734066555060275659441540730179880840068680711039092402469979537402038522869532858210224421954879125281803617171486680299882175622463954938841161683824017764172124148438928242788323301450705633955505182591808014745581257657569980476219657313856171171041106956687416108450931365450698373196534957320986723454445945232416845732305494189207716358085853199984634824143123729540264742981573020172237026058046740201545250287662018382140146169998065636288937211877886621661690578651489040221004254744005525689460483194423394923570500857169107685204978377809144999120496376447004389621794981767672901579794816635242858841182877011991980777649470507584848234893126914722042071134658473351945026030226538176505680011883028482299815999170838410236573499975247752075137709072936793331605370102620992579010729955042839150039536988476316814658001111401786786920802580057225089821741914525126541381743907218686111921778056456742847181643346546263899570276608898254139702386798819800561168979805761661085945938400171610214159378775050985949240013649311708619468421748433514761538254173535727874452760668054213182096783214642043675647412439936425441952983174011449159555969819986536279264099966926245798558475510001
It took 0.02s
Fibonacci 0..20: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]

Excercise

  1. Catalan numbers (info here) are defined by the following recurrence equation:

\[\begin{split}C(n)=\left\{ \begin{array}{ll} 1 & if\ n <=1 \\ \sum_{i=0}^{n-1} C(i) C(n-1 -i)& if\ n > 1 \end{array} \right.\end{split}\]

the first few values are reported below:

\(1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786,\) \(208012, 742900, 2674440, 9694845, 35357670, 129644790,\) \(477638700, 1767263190, 6564120420, 24466267020, 91482563640, ...\)

  1. Write a recursive function recCatalan(n) to compute the n-th catalan number;

  2. Write a dynamic programming function dpCatalan(n) to compute the n-th catalan number.

Test your code with:

catN = []
for i in range(0,15):
    catN.append(recCatalan(i))

print("First 15 catalan numbers:")
print(catN)

Finally, check how long it takes to compute the 20th catalan number with the recursive algorithm and with the dynamic programming one.

Show/Hide Solution

Finding (the optimal) overlaps among DNA strings

As another example of dynamic programming, let’s consider the problem of finding overlaps between two reads. This is quite an important problem for genome assembly and since sequencers nowadays produce several thousands/millions of (long) reads, devising efficient algorithms to find overlaps between two reads is quite important in this field.

Note in fact that, given a set of \(N\) reads, assembly algorithms need to find the best overlaps among all of them, which means testing \(N * (N-1)\) pairs.

Given two reads \(X\) and \(Y\) the optimal overlap among them is the longest suffix of \(X\) that matches (possibly with some mismatches) a prefix of \(Y\).

Example:

image1

We are basically interested in finding the best alignment of a suffix of \(X\) on a prefix of \(Y\) taking possible errors in consideration.

First of all we need to define a score function that given two bases (among the possible 4: A,T,C,G and the gap “-“), returns a score reporting the goodness of the match of the two bases:

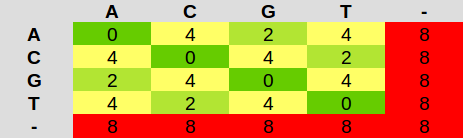
image2

which basically penalizes mismatches by giving them a high score. Our aim would be to find the longest string with the lowest score starting from the end of the first string backwards.

Given the two strings \(X\) and \(Y\), the so called global alignment recurrence is the following:

\[\begin{split}A[i,j]=min \left\{ \begin{array}{l} A[i - 1, j] + score(x[i - 1], "-")\\ A[i, j - 1] + score("-", y[j - 1])\\ A[i - 1 , j - 1] + score(x[i - 1], y[j - 1]) \end{array} \right.\end{split}\]

The first row of the matrix corresponds to “-” in \(X\) and all elements are initialized to \(\infty\), while the first column corresponds to a “-” in \(Y\) and all elements are initialized to 0.

Intuitively, the first row represents the case in which we want to match a base in \(X\) with a gap “-” in \(Y\) (and therefore we do not use characters of \(Y\)), in the second row we match a base in \(Y\) with a gap “-” in \(X\) and in the third we have a base from both.

We can impose a minimum length \(N\) of the overlap by setting to infinity the last \(N-1\) elements of the first column and setting to infinity (at the end) the first \(N\) columns of the last row.

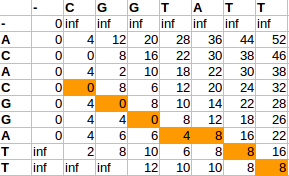
The output of this procedure is a matrix like (where the highlighted elements are actually the overlap):

image3

For now we will see the code that builds the matrix. Obtaining the actual overlap will involve travelling back up from the last row of the matrix

[6]:

import math

def score(a,b):
    mat = {}
    mat["A"] = {"A" : 0, "C" : 4, "G" : 2, "T" : 4, "-" : 8}
    mat["C"] = {"A" : 4, "C" : 0, "G" : 4, "T" : 2, "-" : 8}
    mat["G"] = {"A" : 2, "C" : 4, "G" : 0, "T" : 4, "-" : 8}
    mat["T"] = {"A" : 4, "C" : 2, "G" : 4, "T" : 0, "-" : 8}
    mat["-"] = {"A" : 8, "C" : 8, "G" : 8, "T" : 8, "-" : 8}

    return mat[a][b]


def computeMatrix(X,Y, minLen = 0):
    # + 1 is for leading "-"
    x_len = len(X) + 1
    y_len = len(Y) + 1
    print(X)
    print(Y)

    A = []

    #initialize first column to 0 and first row to infinite
    for i in range(x_len - minLen + 1):
        A.append([0])
    for i in range(minLen - 1):
        A.append([math.inf])
    for i in range(y_len - 1):
        A[0].append(math.inf)

    # compute the rest of the score matrix
    for i in range(1,x_len):
        for j in range(1,y_len):
            c1 = A[i-1][j] + score(X[i-1], "-")
            c2 = A[i][j-1] + score("-", Y[j-1])
            c3 = A[i-1][j-1] + score(X[i-1],Y[j-1])
            #print("i,j: {},{}".format(i,j))
            A[i].append(min([c1,c2,c3]))
    if minLen != 0:
        for i in range(0,minLen):
            A[-1][i] = math.inf
    return A

def plotMatrix(Mat, X,Y):
    X = "-" + X
    outStr = "\t-" +"\t"+ "\t".join(list(Y))

    for i in range(len(X)):
        outStr+="\n" + X[i] +"\t"+ "\t".join([str(x) for x in Mat[i]])
    print(outStr)


X = "CTCGGCCCTAGG"
Y = "GGCTCTAGGCCC"
A = computeMatrix(X,Y,minLen = 5)
print("The overlap matrix:")
plotMatrix(A,X,Y)
print("\n")

X1 = "AATATACATAC"
Y1 = "TACGTACTTA"
B = computeMatrix(X1,Y1, minLen = 4)
print("The overlap matrix:")
plotMatrix(B,X1,Y1)
print("\n")

X3 = "ACACGGATT"
Y3 = "CGGTATT"
D = computeMatrix(X3,Y3, minLen = 3)
print("The overlap matrix:")
plotMatrix(D,X3,Y3)

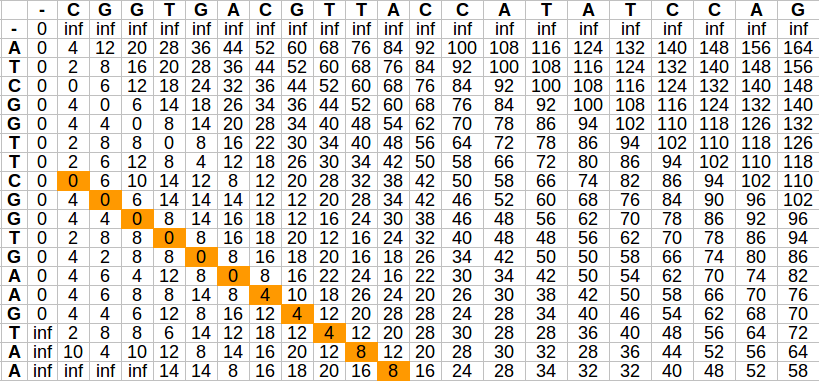
CTCGGCCCTAGG
GGCTCTAGGCCC
The overlap matrix:
        -       G       G       C       T       C       T       A       G       G       C       C       C
-       0       inf     inf     inf     inf     inf     inf     inf     inf     inf     inf     inf     inf
C       0       4       12      20      28      36      44      52      60      68      76      84      92
T       0       4       8       14      20      28      36      44      52      60      68      76      84
C       0       4       8       8       16      20      28      36      44      52      60      68      76
G       0       0       4       12      12      20      24      30      36      44      52      60      68
G       0       0       0       8       16      16      24      26      30      36      44      52      60
C       0       4       4       0       8       16      18      26      30      34      36      44      52
C       0       4       8       4       2       8       16      22      30      34      34      36      44
C       0       4       8       8       6       2       10      18      26      34      34      34      36
T       inf     4       8       10      8       8       2       10      18      26      34      36      36
A       inf     12      6       12      14      12      10      2       10      18      26      34      40
G       inf     20      12      10      16      18      16      10      2       10      18      26      34
G       inf     inf     inf     inf     inf     20      22      18      10      2       10      18      26


AATATACATAC
TACGTACTTA
The overlap matrix:
        -       T       A       C       G       T       A       C       T       T       A
-       0       inf     inf     inf     inf     inf     inf     inf     inf     inf     inf
A       0       4       12      20      28      36      44      52      60      68      76
A       0       4       4       12      20      28      36      44      52      60      68
T       0       0       8       6       14      20      28      36      44      52      60
A       0       4       0       8       8       16      20      28      36      44      52
T       0       0       8       2       10      8       16      22      28      36      44
A       0       4       0       8       4       12      8       16      24      32      36
C       0       2       8       0       8       6       14      8       16      24      32
A       0       4       2       8       2       10      6       14      12      20      24
T       inf     0       8       4       10      2       10      8       14      12      20
A       inf     8       0       8       6       10      2       10      12      18      12
C       inf     inf     inf     inf     8       8       10      2       10      14      20


ACACGGATT
CGGTATT
The overlap matrix:
        -       C       G       G       T       A       T       T
-       0       inf     inf     inf     inf     inf     inf     inf
A       0       4       12      20      28      36      44      52
C       0       0       8       16      22      30      38      46
A       0       4       2       10      18      22      30      38
C       0       0       8       6       12      20      24      32
G       0       4       0       8       10      14      22      28
G       0       4       4       0       8       12      18      26
A       0       4       6       6       4       8       16      22
T       inf     2       8       10      6       8       8       16
T       inf     inf     inf     12      10      10      8       8

Download the complete source file: computeMatrixScore.py

Exercise

  1. Implement the following method:

  • getOverlap(Mat, X,Y) where Mat is the matrix computed with computeMatrix, X and Y are the two strings. The function should:

    • find the rightmost minimum in the last row of the matrix;

    • back track through the matrix moving on the smallest of the neighboring positions (i.e. from A[i,j] move to min(A[i-1,j], A[i-1,j-1], A[i, j-1]) updating the overlap string accordingly. For example, the following matrix:

image1

should produce the overlap:

\[\begin{split}\begin{array}{r} \hline CGGTATT\\ ACACGG-ATT\\ \hline \end{array}\end{split}\]

If needed, feel free to write another method that prints off the overlap.

You can test your methods with the following code:

X = "CTCGGCCCTAGG"
Y = "GGCTCTAGGCCC"
A = computeMatrix(X,Y,minLen = 5)
print("The overlap matrix for {} and {}:".format(X,Y))
plotMatrix(A,X,Y)
(s1,s2,s,e) = getOverlap(A,X,Y)
printAligns(s1,s2,s,e)
print("\n")

X1 = "AATATACATAC"
Y1 = "TACGTACTTA"
B = computeMatrix(X1,Y1, minLen = 4)
print("The overlap matrix for {} and {}:".format(X1,Y1))
plotMatrix(B,X1,Y1)
(s1,s2,s,e) = getOverlap(B,X1,Y1)
printAligns(s1,s2,s,e)
print("\n")

X2 = "ACACGGATT"
Y2 = "CGGTATT"
C = computeMatrix(X2,Y2, minLen = 3)
(s1,s2,s,e) = getOverlap(C,X2,Y2)
printAligns(s1,s2,s,e)
print("\n")

X3 = "GTCAGTCAATCTACTCGGAAACTATACACCG"
Y3 = "AACTATTTCCGTAACACGGATT"
D = computeMatrix(X3,Y3, minLen = 8)
(s1,s2,s,e) = getOverlap(D,X3,Y3)
printAligns(s1,s2,s,e)
print("\n")

X4 = "ATCGGTTCGGTGAAGTAA"
Y4 = "CGGTGACGTTACCATATCCAG"
E = computeMatrix(X4,Y4, minLen = 8)
(s1,s2,s,e) = getOverlap(E,X4,Y4)
printAligns(s1,s2,s,e)

Show/Hide Solution