Module 2, midterm simulation test

This is the second QCB MidTerm exam provided in December 2020.

In the following, you will find the complete text and the solutions for the practical exercises. Please, refer to Alessandro Romanel for any comment on the theoretical part.

Theoretical part

Exercise 1

Given a list 𝐿 of 𝑛≥3 integer elements, please compute the asymptotic computational complexity of the following function, explaining your reasoning.

def my_fun(L):
    for i in range(3, len(L)):
        k = 0
        R = L[i]
        tmp = []
        while k < 3:
            if k % 2 == 1:
                R = R - L[k]
            else:
                R = R + L[k]
            k += 1
        tmp.append(R)

    return sum(tmp)

Exercise 2

What is the topological sorting of a directed acyclic graph (DAG)? Briefly describe an algorithm to compute it and provide a possible topological view of the following DAG.

Practical part

Exercise 3

Guess-sort is a sorting algorithm working as follows:

1. Pick two indices i and j at random; if a[i] > a[j], then swap them.

2. Repeat until the input is sorted.

Implement the GuessSort class by extending the provided SortingAlgorithm class. Test it on a random array of 500 elements and check its correctness. Then, analyze the time complexity of this algorithm.

class SortingAlgorithm:
    def __init__(self, data, verbose = True):
        self.data = data
        self.comparisons = 0
        self.operations = 0
        self.verbose = verbose

    def getData(self):
        return self.data

    def getOperations(self):
        return self.operations

    def getComparisons(self):
        return self.comparisons

    def sort(self):
        raise NotImplementedError

sa = SortingAlgorithm([])
print(sa)
sa.sort()

<__main__.SortingAlgorithm object at 0x7facc31e0c40>

---------------------------------------------------------------------------
NotImplementedError                       Traceback (most recent call last)
Cell In[2], line 22
     20 sa = SortingAlgorithm([])
     21 print(sa)
---> 22 sa.sort()

Cell In[2], line 18, in SortingAlgorithm.sort(self)
     17 def sort(self):
---> 18     raise NotImplementedError

NotImplementedError:

Show/Hide Implementation

import random

class SortingAlgorithm:
    def __init__(self, data, verbose = True):
            self.data = data
            self.comparisons = 0
            self.operations = 0
            self.verbose = verbose

    def getData(self):
            return self.data

    def getOperations(self):
            return self.operations

    def getComparisons(self):
            return self.comparisons

    def sort(self):
            raise NotImplementedError


class GuessSort(SortingAlgorithm):
    def __isSorted(self):
            return all(self.data[i] <= self.data[i+1] for i in range(len(self.data) - 1))

    def sort(self):
            operations = 0
            while (not self.__isSorted()):
                    i = random.randint(0, len(self.data) - 1)
                    j = random.randint(0, len(self.data) - 1)

                    if (((i < j) and self.data[i] > self.data[j]) or ((i > j) and self.data[i] < self.data[j])):
                            self.data[i], self.data[j] = self.data[j], self.data[i]
                            operations += 1

            print("Sorted by doing {} operations".format(operations))


sorter = GuessSort([3,2,5,6,9,7,4])
sorter.sort()
print(sorter.getData())

inList = []
for i in range(500):
    inList.append(random.randint(0,500))

sorter = GuessSort(inList)
sorter.sort()
print('First 20 sorted elements:', sorter.getData()[:20])

Sorted by doing 6 operations
[2, 3, 4, 5, 6, 7, 9]
Sorted by doing 3043 operations
First 20 sorted elements: [1, 2, 4, 6, 9, 13, 13, 16, 17, 17, 18, 18, 19, 19, 20, 21, 23, 23, 25, 26]

The complexity of GuessSort is O(n^2*log2(n)), as the maximum number of bad pairs is O(n^2) and the number of bad pairs decreases with each swap.

Download the complete source file: GuessSort.py

Exercise 4

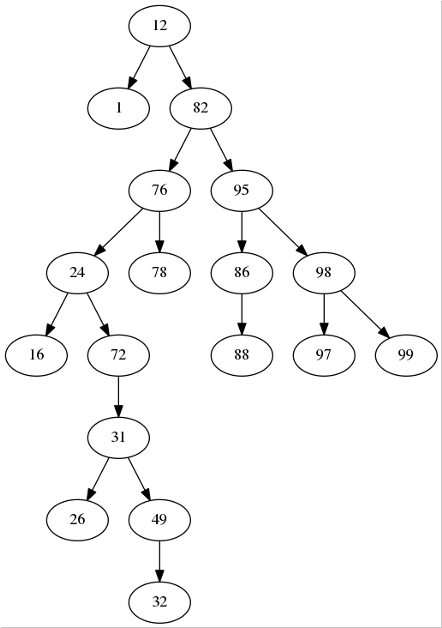
Given a binary search tree as the one provided in the file BST.py, implement the missing function search_interval(a, b) that given two values a and b, finds all values between a and b in the tree, returning them in an ordered data structure. For instance, calling search_interval(24, 33) on the following tree should return: [24, 26, 31, 32].

class BinaryTree:
    def __init__(self, value):
        self.__data = value
        self.__right = None
        self.__left = None
        self.__parent = None
        self.__depth = 0

    def getDepth(self):
        return self.__depth
    def setDepth(self, newdepth):
        self.__depth = newdepth

    def getValue(self):
        return self.__data
    def setValue(self, newValue):
        self.__data = newValue

    def getParent(self):
        return self.__parent
    def setParent(self, tree):
        self.__parent = tree

    def getRight(self):
        return self.__right
    def getLeft(self):
        return self.__left

    def insertRight(self, tree):
        if self.__right == None:
            self.__right = tree
            tree.setParent(self)
            tree.setDepth(self.getDepth() + 1)
    def insertLeft(self, tree):
        if self.__left == None:
            self.__left = tree
            tree.setDepth(self.getDepth() + 1)
            tree.setParent(self)

    def deleteRight(self):
        self.__right = None
    def deleteLeft(self):
        self.__left = None

    def inOrderDFS(self):
        ret = []
        if self != None:
            r = self.getRight()
            l = self.getLeft()
            if l != None:
                ret.extend(l.inOrderDFS())
            ret.append(self.getValue())
            if r != None:
                ret.extend(r.inOrderDFS())
        return ret

    def search_interval(self, a, b):
        raise NotImplementedError

def createBST(intList):
    BST = None
    if len(intList) > 0:
        BST = BinaryTree(intList[0])
        for el in intList[1:]:
            cur_el = BST
            alreadyPresent = False
            prev_el = None
            while cur_el != None:
                prev_el = cur_el
                cv = cur_el.getValue()
                if  cv > el:
                    cur_el = cur_el.getLeft()
                elif cv < el:
                    cur_el = cur_el.getRight()
                else:
                    # cv == el (el is already present)
                    # not allowed by rule c, so skip it
                    alreadyPresent = True
                    #print("El {} already present".format(el))
                    break

            if not alreadyPresent:
                node = BinaryTree(el)
                node.setParent(prev_el)
                if prev_el.getValue() > el:
                    prev_el.insertLeft(node)
                else:
                    prev_el.insertRight(node)

    return BST


def printTree(root):
    cur = root
    #each element is a node and a depth
    #depth is used to format prints (with tabs)
    nodes = [(cur,0)]
    tabs = ""
    lev = 0
    while len(nodes) >0:
        cur, lev = nodes.pop(-1)
        if cur.getRight() != None:
            print ("{}{} (r)-> {}".format("\t"*lev,
                                          cur.getValue(),
                                          cur.getRight().getValue()))
            nodes.append((cur.getRight(), lev+1))
        if cur.getLeft() != None:
            print ("{}{} (l)-> {}".format("\t"*lev,
                                          cur.getValue(),
                                          cur.getLeft().getValue()))
            nodes.append((cur.getLeft(), lev+1))


if __name__ == "__main__":
    import random

    inList = []
    for i in range(1000):
        inList.append(random.randint(0,1000))

    #printTree(createBST(inList[:20])) # to test tree creation...

    BST = createBST(inList)

    sorted = BST.search_interval(24, 33)
    print("Elements between 24 and 33 in the BST:")
    print(sorted)

---------------------------------------------------------------------------
NotImplementedError                       Traceback (most recent call last)
Cell In[4], line 125
    121 #printTree(createBST(inList[:20])) # to test tree creation...
    123 BST = createBST(inList)
--> 125 sorted = BST.search_interval(24, 33)
    126 print("Elements between 24 and 33 in the BST:")
    127 print(sorted)

Cell In[4], line 58, in BinaryTree.search_interval(self, a, b)
     57 def search_interval(self, a, b):
---> 58     raise NotImplementedError

NotImplementedError:

Show/Hide Implementation

class BinaryTree:
    def __init__(self, value):
        self.__data = value
        self.__right = None
        self.__left = None
        self.__parent = None
        self.__depth = 0

    def getDepth(self):
        return self.__depth
    def setDepth(self, newdepth):
        self.__depth = newdepth

    def getValue(self):
        return self.__data
    def setValue(self, newValue):
        self.__data = newValue

    def getParent(self):
        return self.__parent
    def setParent(self, tree):
        self.__parent = tree

    def getRight(self):
        return self.__right
    def getLeft(self):
        return self.__left

    def insertRight(self, tree):
        if self.__right == None:
            self.__right = tree
            tree.setParent(self)
            tree.setDepth(self.getDepth() + 1)
    def insertLeft(self, tree):
        if self.__left == None:
            self.__left = tree
            tree.setDepth(self.getDepth() + 1)
            tree.setParent(self)

    def deleteRight(self):
        self.__right = None
    def deleteLeft(self):
        self.__left = None

    def inOrderDFS(self):
        ret = []
        if self != None:
            r = self.getRight()
            l = self.getLeft()
            if l != None:
                ret.extend(l.inOrderDFS())
            ret.append(self.getValue())
            if r != None:
                ret.extend(r.inOrderDFS())
        return ret

    def search_interval(self, a, b):
        # implemented function!
        greaterThanMin = a < self.__data
        lowerThanMax = b > self.__data

        elements = []

        if greaterThanMin:
            if (self.__left != None):
                elements.extend(self.__left.search_interval(a, b))

        if (a <= self.__data <= b):
            elements.append(self.__data)

        if lowerThanMax:
            if (self.__right != None):
                elements.extend(self.__right.search_interval(a, b))

        return(elements)

def createBST(intList):
    BST = None
    if len(intList) > 0:
        BST = BinaryTree(intList[0])
        for el in intList[1:]:
            cur_el = BST
            alreadyPresent = False
            prev_el = None
            while cur_el != None:
                prev_el = cur_el
                cv = cur_el.getValue()
                if  cv > el:
                    cur_el = cur_el.getLeft()
                elif cv < el:
                    cur_el = cur_el.getRight()
                else:
                    # cv == el (el is already present)
                    # not allowed by rule c, so skip it
                    alreadyPresent = True
                    #print("El {} already present".format(el))
                    break

            if not alreadyPresent:
                node = BinaryTree(el)
                node.setParent(prev_el)
                if prev_el.getValue() > el:
                    prev_el.insertLeft(node)
                else:
                    prev_el.insertRight(node)

    return BST


def printTree(root):
    cur = root
    #each element is a node and a depth
    #depth is used to format prints (with tabs)
    nodes = [(cur,0)]
    tabs = ""
    lev = 0
    while len(nodes) >0:
        cur, lev = nodes.pop(-1)
        if cur.getRight() != None:
            print ("{}{} (r)-> {}".format("\t"*lev,
                                          cur.getValue(),
                                          cur.getRight().getValue()))
            nodes.append((cur.getRight(), lev+1))
        if cur.getLeft() != None:
            print ("{}{} (l)-> {}".format("\t"*lev,
                                          cur.getValue(),
                                          cur.getLeft().getValue()))
            nodes.append((cur.getLeft(), lev+1))


if __name__ == "__main__":
    import random

    inList = []
    for i in range(1000):
        inList.append(random.randint(0,1000))

    #printTree(createBST(inList[:20])) # to test tree creation...

    BST = createBST(inList)

    sorted = BST.search_interval(24, 33)
    print("Elements between 24 and 33 in the BST:")
    print(sorted)

Elements between 24 and 33 in the BST:
[24, 27, 29, 30, 31, 33]

Download the complete source file: BST_complete.py